3 Astuces à connaitre pour investir intelligemment
Tu rêves de faire travailler votre argent, mais tu ignores combien de temps il faudrait pour réellement doubler toncapital ? Tu hésites à investir « plus tard » ? Dans cet article, on décortique la règle des 72 (le raccourci incontournable pour estimer le temps de doublement), je vais te monter, chiffres à l’appui, que cinq années de procrastination peuvent diviser votre patrimoine par deux, puis on utilisera une calculette d’intérêts composés pour tester tes propres scénarios. Que tu débutes en bourse, en crypto ou en immobilier tokenisé, ces trois astuces t’aideront à passer de la théorie à l’action — et à voir comment chaque euro placé aujourd’hui peut se transformer demain. Bonne lecture !
Doubler ton capital : maîtriser la règle des 72
La règle des 72 est le raccourci mental à connaitre pour tous investisseurs afin de savoir en un claquement de doigts combien d’années il faut à un capital pour doubler grâce aux intérêts composés.
Il suffit de diviser 72 par ton taux de rendement annuel :
Années ≈ 72 ÷ taux (en %)
- À 6 % par an ? 72 ÷ 6 ≈ 12 ans.
- À 9 % ? 72 ÷ 9 ≈ 8 ans.
Exemple concret : 1 000 € placés aujourd’hui
| Rendement annuel | Années (règle 72) | Valeur finale après X années |
|---|---|---|
| 3 % | 24 ans | ≈ 2 000 € |
| 5 % | 14 ans | ≈ 2 000 € |
| 7 % | 10 ans | ≈ 2 000 € |
| 10 % | 7 ans | ≈ 2 000 € |
| 12 % | 6 ans | ≈ 2 000 € |
💡 À retenir : plus le taux grimpe, plus l’effet exponentiel s’accélère. Doublant en 7 ans à 10 %, votre capital peut être multiplié par 8 en à peine 21 ans (3 doublages successifs).
D’où vient le chiffre 72 ?
Mathématiquement, le temps nécessaire pour doubler une somme avec un taux r est
n = ln(2) / ln(1 + r)Pour des rendements usuels (4 – 12 %), ln(1 + r) s’approxime bien avec r, et ln(2) vaut 0,693… puis fois 100 car on raisonne en pourcentage, ça donne ≈ 70. On ajoute 2 pour compenser l’arrondi et obtenir un nombre plus divisible (72 = 8 × 9 = 6 × 12).
Astuce de tête : la règle des 70
Si tu as besoin d’un calcul encore plus rapide (ou plutôt plus simple à retenir sans calculatrice et à effectuer de tête, retiens la règle des 70 :
Années ≈ 70 ÷ taux
L’erreur reste inférieure à un an pour des rendements ≤ 9 %. Idéal pour tester instantanément des scénarios (ex. : 8 % → ~ 9 ans au lieu de 9 ans avec la règle 72).
Le coût de la procrastination : 5 ans de retard, un capital quasiment divisé par 2 !
L’un des plus grands ennemis des intérêts composés, c’est le temps perdu. Commencer à investir « quand j’aurai plus d’argent » ou « l’an prochain » peut sembler anodin ; en réalité, quelques années de retard suffisent à éroder la moitié du capital final.
Cas pratique : Investisseur A vs Investisseur B
| Paramètre | Investisseur A – 35 ans | Investisseur B – 30 ans |
|---|---|---|
| Âge de départ début de l’épargne | 25 ans | 30 ans |
| Versement mensuel | 200 € | 200 € |
| Rendement annuel moyen | 10 % | 10 % |
| Âge de retrait arrêt de l’épargne | 60 ans | 60 ans |
| Intérêts générés | ≈ 647 000 € | ≈ 363000 € |
📉 5 ans de décalage → Ton capital aura travaillé 2 fois moins
Pourquoi un tel écart ?
- Intérêts sur intérêts
Les gains des premières années génèrent à leur tour des intérêts. Sans les 5 premières années, vous « coupez » la base de la pyramide exponentielle. - La phase « accélération » commence vers 15–20 ans
C’est à ce moment que la courbe s’envole. En démarrant 5 ans plus tard, vous terminez la course avant ce décollage complet. - Chaque année manquée coûte davantage que la précédente
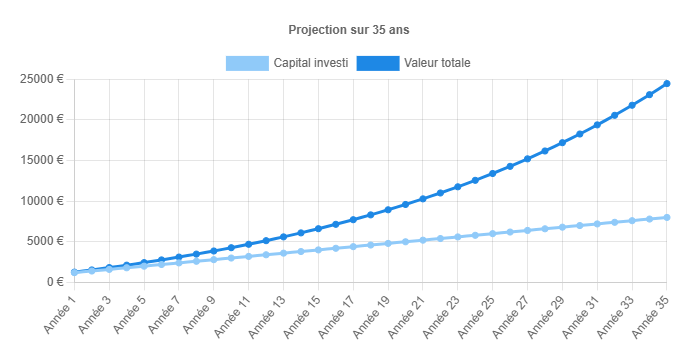
À 10 % de rendement, 10 000 € investis 25 ans rapportent ≈ 196 000 € ; les mêmes 10 000 € investis 20 ans rapportent ≈ 98 000 €.
→ 5 ans “de trop” ≈ 100 000 € perdus dans cet exemple.
Et on dit que les premiers 100 000 sont les plus difficiles … Alors qu’il ne faut que commencer 😉
Comment rattraper le retard ?
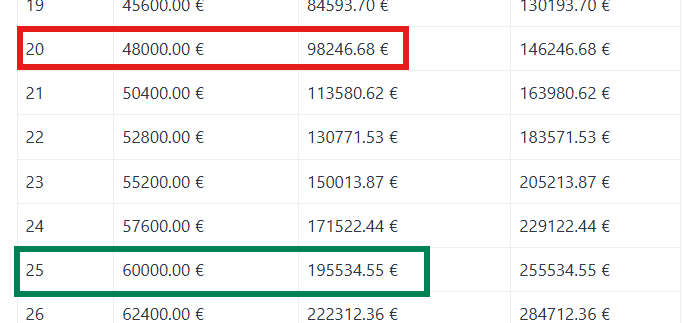
- Augmenter le versement mensuel : pour compenser 5 ans de retard, il faudrait passer de 200 € à ~ 390 € / mois (même rendement).
- Rehausser (prudemment) le rendement attendu : 12 %… mais risque et volatilité suivent la même pente !
Sachant que le rendement annualisé du SP500 sur les 50 dernières années et de 10-12% c’est quasiment impossible à tenir sur notre période de 35 ans - Automatiser l’épargne : mettre en place un virement automatique dès le salaire reçu supprime la tentation de reporter encore.
Moralité : le meilleur moment, c’était hier… le deuxième meilleur, c’est aujourd’hui.
Plus tôt vous laissez agir les intérêts composés, plus votre capital « travaille » longtemps pour vous. Même de petites sommes placées tôt battent des versements plus gros mais tardifs.
C’est pour ça que j’utilise des outils qui me permettent d’épargner à faible coût
Dès que tu as fais 5 achats, envoi moi un email et…
5 USDC en cadeau, soit le rendement annuel d’un token déjà assuré!
Ma petite touche perso de la fameuse citation:
Le meilleur moment, c’était hier… le deuxième meilleur, c’est aujourd’hui…
et le pire moment, c’est demain !
😉
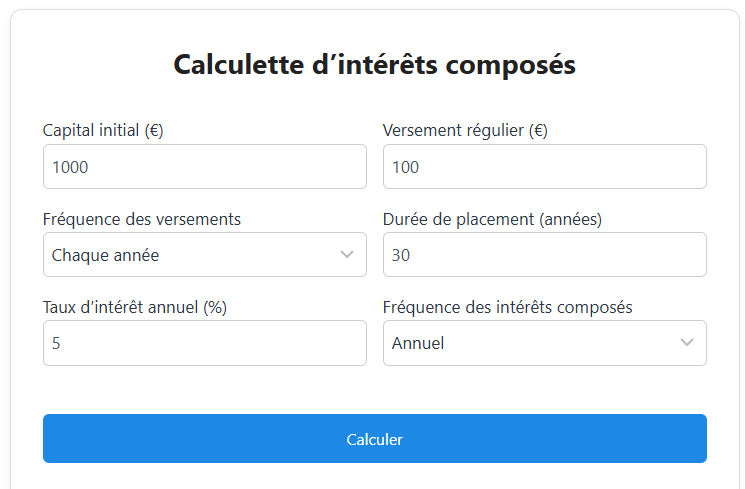
Calculette d’intérêts composés : projetez vos scénarios en un clic
Les règles de 70 / 72 et les exemples chiffrés montrent la puissance des intérêts composés… mais rien ne vaut une projection personnalisée. Changer :
- le montant de départ,
- les versements réguliers,
- la durée,
- le taux de rendement,
peut faire varier le capital final du simple au triple.
Pourquoi simuler ?
| Paramètre | Impact direct | Exemple (200 €/mois, 10 %) |
|---|---|---|
| Commencer 5 ans plus tôt | +100 % 🤯 | 452 k€ → 759 k€ |
| Ajouter +50 €/mois | +25 % malgré même rendement | 759 k€ → 948 k€ |
| Gagner 1 pt de rendement | Effet boule de neige | 10 % → 11 % = +200 k€ sur 35 ans |
Sans calculette, il est impossible d’apprécier ces écarts d’un simple coup d’œil.
Comment utiliser la calculette
- Indiquez votre capital initial (ex. : 5 000 €).
- Choisissez la fréquence de versement (mensuel, trimestriel…) et le montant.
- Réglez la durée avec le curseur (en années).
- Sélectionnez le taux de rendement estimé.
▶️ Clique sur Calculer : un graphique interactif s’affiche, accompagné d’un tableau récapitulatif année par année.
Testez vos propres scénarios
🔗 Essaye la calculette d’intérêts composés ici : Calculette d’intérêts composés
Comparez, par exemple :
- 250 €/mois à 8 % sur 25 ans
- vs 200 €/mois à 10 % sur 20 ans
Vous verrez immédiatement quel scénario correspond le mieux à votre objectif, et combien “coûte” chaque année d’attente.
La règle des 72 te donne l’intuition, la comparaison A vs B prouve l’urgence de commencer, et la calculette transforme ces notions en plans d’action chiffrés.
Commence petit, commence tôt… mais surtout, commence aujourd’hui !